Скалярное произведение определение. Формула скалярного произведения векторов для плоских задач

Скалярное произведение векторов (далее в тексте СП). Дорогие друзья! В состав экзамена по математике входит группа задач на решение векторов. Некоторые задачи мы уже рассмотрели. Можете посмотреть их в категории «Векторы». В целом, теория векторов несложная, главное последовательно её изучить. Вычисления и действия с векторами в школьном курсе математики просты, формулы не сложные. Загляните в . В этой статье мы разберём задачи на СП векторов (входят в ЕГЭ). Теперь «погружение» в теорию:

Ч тобы найти координаты вектора, нужно из координат его конца вычесть соответствующие координаты его начала

И ещё:

*Длина вектора (модуль) определяется следующим образом:

Данные формулы необходимо запомнить!!!

Покажем угол между векторами:

Понятно, что он может изменяться в пределах от 0 до 180 0 (или в радианах от 0 до Пи).

Можем сделать некоторые выводы о знаке скалярного произведения. Длины векторов имеют положительное значение, это очевидно. Значит знак скалярного произведения зависит от значения косинуса угла между векторами.

Возможны случаи:

1. Если угол между векторами острый (от 0 0 до 90 0), то косинус угла будет иметь положительное значение.

2. Если угол между векторами тупой (от 90 0 до 180 0), то косинус угла будет иметь отрицательное значение.

*При нуле градусов, то есть когда векторы имеют одинаковое направление, косинус равен единице и соответственно результат будет положительным.

При 180 о, то есть когда векторы имеют противоположные направления, косинус равен минус единице, и соответственно результат будет отрицательным.

Теперь ВАЖНЫЙ МОМЕНТ!

При 90 о, то есть когда векторы перпендикулярны друг другу, косинус равен нулю, а значит и СП равно нулю. Этот факт (следствие, вывод) используется при решение многих задач, где речь идёт о взаимном расположении векторов, в том числе и в задачах входящих в открытый банк заданий по математике.

Сформулируем утверждение: скалярное произведение равно нулю тогда и только тогда, когда данные векторы лежат на перпендикулярных прямых.

Итак, формулы СП векторов:

Если известны координаты векторов или координаты точек их начал и концов, то всегда сможем найти угол между векторами:

Рассмотрим задачи:

27724 Найдите скалярное произведение векторов a и b .

Скалярное произведение векторов мы можем найти по одной из двух формул:

Угол между векторами неизвестен, но мы без труда можем найти координаты векторов и далее воспользоваться первой формулой. Так как начала обоих векторов совпадают с началом координат, то координаты данных векторов равны координатам их концов, то есть

Как найти координаты вектора изложено в .

Вычисляем:

Ответ: 40

Найдём координаты векторов и воспользуемся формулой:

Чтобы найти координаты вектора необходимо из координат конца вектора вычесть соответствующие координаты его начала, значит

Вычисляем скалярное произведение:

Ответ: 40

Найдите угол между векторами a и b . Ответ дайте в градусах.

Пусть координаты векторов имеют вид:

Для нахождения угла между векторами используем формулу скалярного произведения векторов:

Косинус угла между векторами:

Следовательно:

Координаты данных векторов равны:

Подставим их в формулу:

Угол между векторами равен 45 градусам.

Ответ: 45

Лекция: Координаты вектора; скалярное произведение векторов; угол между векторами

Координаты вектора

Итак, как уже говорилось ранее, вектора – это направленный отрезок, у которого есть собственное начало и конец. Если начало и конец представлены некоторыми точками, значит на плоскости или в пространстве у них есть свои координаты.

Если же у каждой точки есть свои координаты, то мы можем получить и координаты целого вектора.

Допустим, мы имеем некоторый вектор, у которого начало и конец вектора имеют следующие обозначения и координаты: A(A x ; Ay) и B(B x ; By)

Чтобы получить координаты данного вектора, необходимо из координат конца вектора вычесть соответствующие координаты начала:

Для определения координаты вектора в пространстве следует воспользоваться следующей формулой:

Скалярное произведение векторов

Существует два способа определения понятия скалярного произведения:

• Геометрический способ. Согласно ему, скалярное произведение равно произведению величин данных модулей на косинус угла между ними.

• Алгебраический смысл. С точки зрения алгебры, скалярное произведение двух вектором – это некая величина, которая получается в результате суммы произведений соответствующих векторов.

Если векторы заданы в пространстве, то следует воспользоваться аналогичной формулой:

Свойства:

• Если умножить два одинаковых вектора скалярно, то их скалярное произведение будет не отрицательным:

• Если же скалярное произведение двух одинаковых векторов получилось равным нулю, то эти векторы считаются нулевыми:

• Если некоторый вектор умножить на себя же, то скалярное произведение получится равным квадрату его модуля:

• Скалярное произведение имеет коммуникативное свойство, то есть от перестановки векторов скалярное произведение не изменится:

• Скалярное произведение ненулевых векторов может быть равно нулю только в том случае, если вектора перпендикулярны друг другу:

• Для скалярного произведения векторов справедлив переместительный закон в случае с умножением одного из векторов на число:

• При скалярном произведении так же можно использовать дистрибутивное свойство умножения:

Угол между векторами

Если в задаче и длины векторов, и угол между ними преподнесены "на блюдечке с голубой каёмочкой", то условие задачи и её решение выглядят так:

Пример 1. Даны векторы . Найти скалярное произведение векторов , если их длины и угол между ними представлены следующими значениями:

Справедливо и другое определение, полностью равносильное определению 1.

Определение 2 . Скалярным произведением векторов называется число (скаляр), равное произведению длины одного их этих векторов на проекцию другого вектора на ось, определяемую первым из указанных векторов. Формула согласно определению 2:

Задачу с применением этой формулы решим после следующего важного теоретического пункта.

Определение скалярного произведения векторов через координаты

То же самое число можно получить, если перемножаемые векторы заданы своими координатами.

Определение 3. Скалярное произведение векторов - это число, равное сумме попарных произведений их соответствующих координат .

На плоскости

Если два вектора и на плоскости определены своими двумя декартовыми прямоугольными координатами

то скалярное произведение этих векторов равно сумме попарных произведений их соответствующих координат:

.

Пример 2. Найти численную величину проекции вектора на ось, параллельную вектору .

Решение. Находим скалярное произведение векторов, складывая попарные произведения их координат:

Теперь нам требуется приравнять полученное скалярное произведение произведению длины вектора на проекцию вектора на ось, параллельную вектору (в соответствии с формулой ).

Находим длину вектора как квадратный корень из суммы квадратов его координат:

.

Составляем уравнение и решаем его:

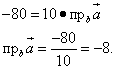
Ответ. Искомая численная величина равна минус 8.

В пространстве

Если два вектора и в пространстве определены своими тремя декартовыми прямоугольными координатами

,

то скалярное произведение этих векторов также равно сумме попарных произведений их соответствующих координат, только координат уже три:

.

Задача на нахождение скалярного произведения рассмотренным способом - после разбора свойств скалярного произведения. Потому что в задаче потребуется определить, какой угол образуют перемножаемые векторы.

Свойства скалярного произведения векторов

Алгебраические свойства

1. (переместительное свойство : от перемены местами перемножаемых векторов величина их скалярного произведения не меняется).

2. (сочетательное относительно числового множителя свойство : скалярное произведение вектора, умноженного на некоторый множитель, и другого вектора, равно скалярному произведению этих векторов, умноженному на тот же множитель).

3. (распределительное относительно суммы векторов свойство : скалярное произведение суммы двух векторов на третий вектор равно сумме скалярных произведений первого вектора на третий вектор и второго вектора на третий вектор).

4. (скалярный квадрат вектора больше нуля ), если - ненулевой вектор, и , если - нулевой вектор.

Геометрические свойства

В определениях изучаемой операции мы уже касались понятия угла между двумя векторами. Пора уточнить это понятие.

На рисунке выше видны два вектора, которые приведены к общему началу. И первое, на что нужно обратить внимание: между этими векторами существуют два угла - φ 1 и φ 2 . Какой из этих углов фигурирует в определениях и свойствах скалярного произведения векторов? Сумма рассмотренных углов равна 2π и поэтому косинусы этих углов равны. В определение скалярного произведения входит только косинус угла, а не значение его выражения. Но в свойствах рассматривается только один угол. И это тот из двух углов, который не превосходит π , то есть 180 градусов. На рисунке этот угол обозначен как φ 1 .

1. Два вектора называют ортогональными и угол между этими векторами - прямой (90 градусов или π /2 ), если скалярное произведение этих векторов равно нулю :

.

Ортогональностью в векторной алгебре называется перпендикулярность двух векторов.

2. Два ненулевых вектора составляют острый угол (от 0 до 90 градусов, или, что тоже самое - меньше π скалярное произведение положительно .

3. Два ненулевых вектора составляют тупой угол (от 90 до 180 градусов, или, что то же самое - больше π /2 ) тогда и только тогда, когда их скалярное произведение отрицательно .

Пример 3. В координатах даны векторы:

.

Вычислить скалярные произведения всех пар данных векторов. Какой угол (острый, прямой, тупой) образуют эти пары векторов?

Решение. Вычислять будем путём сложения произведений соответствующих координат.

Получили отрицательное число, поэтому векторы образуют тупой угол.

Получили положительное число, поэтому векторы образуют острый угол.

Получили нуль, поэтому векторы образуют прямой угол.

Получили положительное число, поэтому векторы образуют острый угол.

.

Получили положительное число, поэтому векторы образуют острый угол.

Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними .

Пример 4. Даны длины двух векторов и угол между ними:

.

Определить, при каком значении числа векторы и ортогональны (перпендикулярны).

Решение. Перемножим векторы по правилу умножения многочленов:

Теперь вычислим каждое слагаемое:

.

Составим уравнение (равенство произведения нулю), приведём подобные члены и решим уравнение:

Ответ: мы получили значение λ = 1,8 , при котором векторы ортогональны.

Пример 5. Доказать, что вектор ортогонален (перпендикулярен) вектору

Решение. Чтобы проверить ортогональность, перемножим векторы и как многочлены, подставляя вместо его выражение, данное в условии задачи:

.

Для этого нужно каждый член (слагаемое) первого многочлена умножить на каждый член второго и полученные произведения сложить:

.

В полученном результате дробь за счёт сокращается. Получается следующий результат:

Вывод: в результате умножения получили нуль, следовательно, ортогональность (перпендикулярность) векторов доказана.

Решить задачу самостоятельно, а затем посмотреть решение

Пример 6. Даны длины векторов и , a угол между этими векторами равен π /4 . Определить, при каком значении μ векторы и взаимно перпендикулярны.

Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними .

Матричное представление скалярного произведения векторов и произведение n-мерных векторов

Иногда выигрышным для наглядности является представление двух перемножаемых векторов в виде матриц. Тогда первый вектор представлен в виде матрицы-строки, а второй - в виде матрицы-столбца:

Тогда скалярное произведение векторов будет произведением этих матриц :

Результат тот же, что и полученный способом, который мы уже рассмотрели. Получили одно единственное число, и произведение матрицы-строки на матрицу-столбец также является одним единственным числом.

В матричной форме удобно представлять произведение абстрактных n-мерных векторов. Так, произведение двух четырёхмерных векторов будет произведением матрицы-строки с четырьмя элементами на матрицу-столбец также с четырьмя элементами, произведение двух пятимерных векторов - произведением матрицы-строки с пятью элементами на матрицу-столбец также с пятью элементами и так далее.

Пример 7. Найти скалярные произведения пар векторов

,

используя матричное представление.

Решение. Первая пара векторов. Представляем первый вектор в виде матрицы-строки, а второй - в виде матрицы-столбца. Находим скалярное произведение этих векторов как произведение матрицы-строки на матрицу-столбец:

Аналогично представляем вторую пару и находим:

Как видим, результаты получились те же, что и у тех же пар из примера 2.

Угол между двумя векторами

Вывод формулы косинуса угла между двумя векторами очень красив и краток.

Чтобы выразить скалярное произведение векторов

(1)

в координатной форме, предварительно найдём скалярные произведение ортов. Скалярное произведение вектора на само себя по определению:

То, что записано в формуле выше, означает: скалярное произведение вектора на самого себя равно квадрату его длины . Косинус нуля равен единице, поэтому квадрат каждого орта будет равен единице:

Так как векторы

попарно перпендикулярны, то попарные произведения ортов будут равны нулю:

Теперь выполним умножение векторных многочленов:

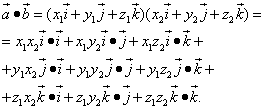
Подставляем в правую часть равенства значения соответствующих скалярных произведений ортов:

Получаем формулу косинуса угла между двумя векторами:

Пример 8. Даны три точки A (1;1;1), B (2;2;1), C (2;1;2).

Найти угол .

Решение. Находим координаты векторов:

,

.

По формуле косинуса угла получаем:

Следовательно, .

Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними .

Пример 9. Даны два вектора

Найти сумму, разность, длину, скалярное произведение и угол между ними.

2.Разность

Угол между векторами

Рассмотрим два данных вектора $\overrightarrow{a}$ и $\overrightarrow{b}$. Отложим от произвольно выбранной точки $O$ векторы $\overrightarrow{a}=\overrightarrow{OA}$ и $\overrightarrow{b}=\overrightarrow{OB}$, тогда угол $AOB$ называется углом между векторами $\overrightarrow{a}$ и $\overrightarrow{b}$ (рис. 1).

Рисунок 1.

Отметим здесь, что если векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ сонаправлены или один из них является нулевым вектором, тогда угол между векторами равен $0^0$.

Обозначение: $\widehat{\overrightarrow{a},\overrightarrow{b}}$

Понятие скалярного произведения векторов

Математически это определение можно записать следующим образом:

Скалярное произведение может равняться нулю в двух случаях:

Если один из векторов будет нулевым вектором (Так как тогда его длина равна нулю).

Если векторы будут взаимно перпендикулярны (то есть $cos{90}^0=0$).

Отметим также, что скалярное произведение больше нуля, если угол между этими векторами острый (так как ${cos \left(\widehat{\overrightarrow{a},\overrightarrow{b}}\right)\ } >0$), и меньше нуля, если угол между этими векторами тупой (так как ${cos \left(\widehat{\overrightarrow{a},\overrightarrow{b}}\right)\ }

С понятием скалярного произведения связано понятие скалярного квадрата.

Определение 2

Скалярным квадратом вектора $\overrightarrow{a}$ называется скалярное произведение этого вектора самого на себя.

Получаем, что скалярный квадрат равен

\[\overrightarrow{a}\overrightarrow{a}=\left|\overrightarrow{a}\right|\left|\overrightarrow{a}\right|{cos 0^0\ }=\left|\overrightarrow{a}\right|\left|\overrightarrow{a}\right|={\left|\overrightarrow{a}\right|}^2\]

Вычисление скалярного произведения по координатам векторов

Помимо стандартного способа нахождения значения скалярного произведения, который вытекает из определения, существует еще один способ.

Рассмотрим его.

Пусть векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ имеют координаты $\left(a_1,b_1\right)$ и $\left(a_2,b_2\right)$, соответственно.

Теорема 1

Скалярное произведение векторов $\overrightarrow{a}$ и $\overrightarrow{b}$ равно сумме произведений соответствующих координат.

Математически это можно записать следующим образом

\[\overrightarrow{a}\overrightarrow{b}=a_1a_2+b_1b_2\]

Доказательство.

Теорема доказана.

Эта теорема имеет несколько следствий:

Следствие 1: Векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ перпендикулярны тогда и только тогда, когда $a_1a_2+b_1b_2=0$

Следствие 2: Косинус угла между векторами равен $cos\alpha =\frac{a_1a_2+b_1b_2}{\sqrt{a^2_1+b^2_1}\cdot \sqrt{a^2_2+b^2_2}}$

Свойства скалярного произведения векторов

Для любых трех векторов и действительного числа $k$ справедливо:

${\overrightarrow{a}}^2\ge 0$

Данное свойство следует из определения скалярного квадрата (определение 2).

Переместительный закон: $\overrightarrow{a}\overrightarrow{b}=\overrightarrow{b}\overrightarrow{a}$.

Данное свойство следует из определения скалярного произведения (определение 1).

Распределительный закон:

$\left(\overrightarrow{a}+\overrightarrow{b}\right)\overrightarrow{c}=\overrightarrow{a}\overrightarrow{c}+\overrightarrow{b}\overrightarrow{c}$. \end{enumerate}

По теореме 1, имеем:

\[\left(\overrightarrow{a}+\overrightarrow{b}\right)\overrightarrow{c}=\left(a_1+a_2\right)a_3+\left(b_1+b_2\right)b_3=a_1a_3+a_2a_3+b_1b_3+b_2b_3==\overrightarrow{a}\overrightarrow{c}+\overrightarrow{b}\overrightarrow{c}\]

Сочетательный закон: $\left(k\overrightarrow{a}\right)\overrightarrow{b}=k(\overrightarrow{a}\overrightarrow{b})$. \end{enumerate}

По теореме 1, имеем:

\[\left(k\overrightarrow{a}\right)\overrightarrow{b}=ka_1a_2+kb_1b_2=k\left(a_1a_2+b_1b_2\right)=k(\overrightarrow{a}\overrightarrow{b})\]

Пример задачи на вычисление скалярного произведения векторов

Пример 1

Найти скалярное произведение векторов $\overrightarrow{a}$ и $\overrightarrow{b}$, если $\left|\overrightarrow{a}\right|=3$ и $\left|\overrightarrow{b}\right|=2$, а угол между ними равен ${{30}^0,\ 45}^0,\ {90}^0,\ {135}^0$.

Решение.

Используя определение 1, получаем

Для ${30}^0:$

\[\overrightarrow{a}\overrightarrow{b}=6{cos \left({30}^0\right)\ }=6\cdot \frac{\sqrt{3}}{2}=3\sqrt{3}\]

Для ${45}^0:$

\[\overrightarrow{a}\overrightarrow{b}=6{cos \left({45}^0\right)\ }=6\cdot \frac{\sqrt{2}}{2}=3\sqrt{2}\]

Для ${90}^0:$

\[\overrightarrow{a}\overrightarrow{b}=6{cos \left({90}^0\right)\ }=6\cdot 0=0\]

Для ${135}^0:$

\[\overrightarrow{a}\overrightarrow{b}=6{cos \left({135}^0\right)\ }=6\cdot \left(-\frac{\sqrt{2}}{2}\right)=-3\sqrt{2}\]

Таким образом, длина вектора рассчитывается, как корень квадратный из суммы квадратов его координат
. Аналогично рассчитывается длинаn-мерного вектора
. Если вспомнить, что каждая координата вектора – это разность между координатами конца и начала, то мы получим формулу длины отрезка, т.е. евклидова расстояния между точками.

Скалярное произведение двух векторов на плоскости – это произведение длин этих векторов на косинус угла между ними:
. Можно доказать, что скалярное произведение двух векторов= (х 1 , х 2) и= (y 1 , y 2) равно сумме произведений соответствующих координат этих векторов:
= х 1 * y 1 + х 2 * y 2 .

В n-мерном пространстве скалярное произведение векторовX= (х 1 , х 2 ,...,х n) иY= (y 1 , y 2 ,...,y n) определяется, как сумма произведений их соответствующих координат:X*Y= х 1 * y 1 + х 2 * y 2 + ... + х n * y n .

Операция умножения векторов друг на другу аналогична умножению матрицы-строки на матрицу-столбец. Подчеркнем, что в результате будет получено число, а не вектор.

Скалярное произведение векторов обладает следующими свойствами (аксиомы):

1) Коммутативное свойство: X*Y=Y*X.

2) Дистрибутивное относительно сложения свойство: X(Y+Z) =X*Y+X*Z.

3) Для любого действительного числа 
.

4)
, еслиX– не нулевой вектор;
еслиX– нулевой вектор.

Линейное векторное пространство, в котором задано скалярное произведение векторов, удовлетворяющее четырем соответствующим аксиомам, называется евклидовым линейным векторным пространством .

Легко заметить, что при умножении любого вектора самого на себя мы получим квадрат его длины . Поэтому по-другомудлину вектора можно определить, как корень квадратный из его скалярного квадрата:.

Длина вектора обладает следующими свойствами:

1) |X| = 0Х = 0;

2) |X| = ||*|X|, где– действительное число;

3) |X*Y||X|*|Y| (неравенство Коши-Буняковского );

4) |X+Y||X|+|Y| (неравенство треугольника ).

Угол между векторами вn-мерном пространстве определяется, исходя из понятия скалярного произведения. В самом деле, если
, то
. Эта дробь не больше единицы (согласно неравенству Коши-Буняковского), поэтому отсюда можно найти.

Два вектора называют ортогональными илиперпендикулярными , если их скалярное произведение равно нулю. Из определения скалярного произведения следует, что нулевой вектор ортогонален любому вектору. Если оба ортогональных вектора ненулевые, то обязательноcos= 0, т.е=/2 = 90 о.

Рассмотрим еще раз рисунок 7.4. Из рисунка видно, что косинус угла наклона вектора к горизонтальной оси можно рассчитать как
, а косинус угланаклона вектора к вертикальной оси как
. Эти числа принято называтьнаправляющими косинусами . Легко убедиться, что сумма квадратов направляющих косинусов всегда равна единице:cos 2 +cos 2 = 1. Аналогично можно ввести понятия направляющих косинусов и для пространств большей размерности.

Базис векторного пространства

Для векторов можно определить понятия линейной комбинации ,линейной зависимости инезависимости аналогично тому, как эти понятия были введены для строк матрицы. Также справедливо, что если векторы линейно зависимы, то по крайней мере один из них можно линейно выразить через остальные (т.е. он является их линейной комбинацией). Верно и обратное утверждение: если один из векторов является линейной комбинацией остальных, то все эти векторы в совокупности линейно зависимы.

Отметим, что если среди векторов a l , a 2 ,...a m есть нулевой вектор, то эта совокупность векторов обязательно линейно зависима. В самом деле, мы получим l a l + 2 a 2 +...+ m a m = 0, если, например, приравняем коэффициент j при нулевом векторе к единице, а все остальные коэффициенты – к нулю. При этом не все коэффициенты будут равны нулю ( j ≠ 0).

Кроме того, если какая-то часть векторов из совокупности векторов линейно зависимы, то и все эти вектора - линейно зависимы. В самом деле, если какие-то вектора дают нулевой вектор в своей линейной комбинации с коэффициентами, которые не являются одновременно нулевыми, то к этой сумме произведений можно добавить остальные вектора, умноженные на нулевые коэффициенты, и она по-прежнему будет нулевым вектором.

Как определить, являются ли вектора линейно зависимыми?

Например, возьмем три вектора: а 1 = (1, 0, 1, 5), а 2 = (2, 1, 3, -2) и а 3 = (3, 1, 4, 3). Составим из них матрицу, в которой они будут являться столбцами:

Тогда вопрос о линейной зависимости сведется к определению ранга этой матрицы. Если он окажется равным трем, то все три столбца – линейно независимы, а если окажется меньше, то это будет говорить о линейной зависимости векторов.

Так как ранг равен 2, вектора линейно зависимы.

Отметим, что решение задачи можно было бы начать и с рассуждений, которые основаны на определении линейной независимости. А именно, составить векторное уравнение  l a l + 2 a 2 + 3 a 3 = 0, которое примет вид l *(1, 0, 1, 5) + 2 *(2, 1, 3, -2) + 3 *(3, 1, 4, 3) = (0, 0, 0, 0). Тогда мы получим систему уравнений:

Решение этой системы методом Гаусса сведется к получению той же самой ступенчатой матрицы, только в ней будет еще один столбец – свободных членов. Они все будут равны нулю, так как линейные преобразования нулей не могут привести к другому результату. Преобразованная система уравнений примет вид:

Решением этой системы будет (-с;-с; с), где с – произвольное число; например, (-1;-1;1). Это означает, что если взять  l = -1; 2 =-1 и 3 = 1, то l a l + 2 a 2 + 3 a 3 = 0, т.е. вектора на самом деле линейно зависимы.

Из решенного примера становится ясно, что если взять число векторов больше, чем размерность пространства, то они обязательно будут линейно зависимы. В самом деле, если бы в этом примере мы взяли пять векторов, то получили бы матрицу 4 х 5, ранг которой не мог бы оказаться больше четырех. Т.е. максимальное число линейно независимых столбцов все равно не было бы больше четырех. Два, три или четыре четырехмерных вектора могут оказаться линейно независимыми, а пять и больше – не могут. Следовательно, на плоскости могут оказаться линейно независимыми не более двух векторов. Любые три вектора в двумерном пространстве – линейно зависимы. В трехмерном пространстве любые четыре (или более) вектора – всегда линейно зависимы. И т.п.

Поэтому размерность пространства можно определить, как максимальное число линейно независимых векторов, которые могут в нем быть.

Совокупность n линейно независимых векторов n-мерного пространства R называют базисом этого пространства.

Теорема. Каждый вектор линейного пространства можно представить в виде линейной комбинации векторов базиса, и притом единственным способом.

Доказательство. Пусть векторы e l , e 2 ,...e n образуют базисn-мерного пространства R. Докажем, что любой вектор Х является линейной комбинацией этих векторов. Поскольку вместе с вектором Х число векторов станет (n +1), эти (n +1) векторов будут линейно зависимы, т.е. существуют числа l , 2 ,..., n ,, не равные одновременно нулю, такие что

 l e l + 2 e 2 +...+ n e n +Х = 0

При этом 0, т.к. в противном случае мы получили бы l e l + 2 e 2 +...+ n e n = 0, где не все коэффициенты l , 2 ,..., n равны нулю. Это означает, что векторы базиса оказались бы линейно зависимы. Следовательно, можно разделить обе части первого уравнения на:

( l /)e l + ( 2 /)e 2 +...+ ( n /)e n + Х = 0

Х = -( l /)e l - ( 2 /)e 2 -...- ( n /)e n

Х = x l e l +x 2 e 2 +...+x n e n ,

где х j = -( j /),
.

Теперь докажем, что такое представление в виде линейной комбинации является единственным. Предположим противное, т.е. что существует другое представление:

Х = y l e l +y 2 e 2 +...+y n e n

Вычтем из него почленно полученное ранее выражение:

0 = (y l – х 1)e l + (y 2 – х 2)e 2 +...+ (y n – х n)e n

Так как векторы базиса линейно независимы, получим, что (y j - х j) = 0,
, т.е.y j = х j . Итак, выражение оказалось тем же самым. Теорема доказана.

Выражение Х = x l e l +x 2 e 2 +...+x n e n называютразложением вектора Х по базису e l , e 2 ,...e n , а числа х l , х 2 ,...х n -координатами вектора х относительно этого базиса, или в этом базисе.

Можно доказать, что если nненулевых векторовn-мерного евклидова пространства попарно ортогональны, то они образуют базис. В самом деле, умножим обе части равенства l e l + 2 e 2 +...+ n e n = 0 на любой вектор е i . Получим  l (e l *е i) +  2 (e 2 *е i) +...+  n (e n *е i) = 0   i (e i *е i) = 0   i = 0 для  i.

Векторы e l , e 2 ,...e n n-мерного евклидова пространства образуютортонормированный базис , если эти векторы попарно ортогональны и норма каждого из них равна единице, т.е. если е i *e j = 0 приi≠jи |е i | = 1 дляi.

Теорема (без доказательства). Во всяком n-мерном евклидовом пространстве существует ортонормированный базис.

Примером ортонормированного базиса являют система n единичных векторов е i , у которыхi-я компонента равна единице, а остальные компоненты равны нулю. Каждый такой вектор называетсяорт . Например, вектора-орты (1, 0, 0), (0, 1, 0) и (0, 0, 1) образуют базис трехмерного пространства.