Возникает задача о численном вычислении определенного интеграла, решаемая с помощью формул, носящих название квад­ратурных.

Напомним простейшие формулы численного интегрирования.

Вычислим приближенное численное значение . Интервал интегрирования [а, b] разобьем на п равных частей точками деле­ния
, называемыми узлами квадра­турной формулы. Пусть в узлах известны значения
:

Величина

называется интервалом интегрирования или шагом. Отметим, что в практике -вычислений число я выбирают небольшим, обычно оно не больше 10-20.На частичном интервале

подынтегральную функцию заменяют интерполяционным много­членом

который на рассматриваемом интервале приближенно представ­ляет функцию f (х).

а) Удержим в интерполяционном многочлене только один первый член, тогда

Полученная квадратная формула

называется формулой прямоугольников.

б) Удержим в интерполяционном многочлене два первых члена, тогда

(2)

Формула (2) называется формулой трапеций.

в) Интервал интегрирования
разобьем на четное число 2n равных частей, при этом шаг интегрирования h будет равен. На интервале
длиной 2h подынтегральную функцию заменим интерполяционным многочленом второй сте­пени, т. е. удержим в многочлене три первых члена:

Полученная квадратурная формула называется формулой Симп­сона

(3)

Формулы (1), (2) и (3) имеют простой геометрический смысл. В формуле прямоугольников подынтегральная функция f(х) на интервале
заменяется отрезком прямой у = ук, параллельной оси абсцисс, а в формуле трапеций - отрезком прямой
и вычисляется соответственно площадь прямо­угольника и прямолинейной трапеции, которые затем сумми­руются. В формуле Симпсона функция f(х) на интервале
длиной 2h заменяется квадратным трехчленом - параболой
вычисляется площадь криволинейной параболической трапеции, затем площади суммируются.

ЗАКЛЮЧЕНИЕ

В завершении работы, хочется отметить ряд особенностей применения рассмотренных выше методов. Каждый способ приближённого решения определённого интеграла имеет свои преимущества и недостатки, в зависимости от поставленной задачи следует использовать конкретные методы.

Метод замены переменных является одним из основных методов вычисления неопределенных интегралов. Даже в тех случаях, когда мы интегрируем каким-либо другим методом, нам часто приходится в промежуточных вычислениях прибегать к замене переменных. Успех интегрирования зависит в значительной степени от того, сумеем ли мы подобрать такую удачную замену переменных, которая упростила бы данный интеграл.

По существу говоря изучение методов интегрирования сводится к выяснению того, какую надо сделать замену переменной при том или ином виде подынтегрального выражения.

Таким образом, интегрирование всякой рациональной дроби сводится к интегрированию многочлена и нескольких простейших дробей.

Интеграл от любой рациональной функции может быть выражен через элементарные функции в конечном виде, а именно:

через логарифмы- в случаях простейших дробей 1 типа;

через рациональные функции- в случае простейших дробей 2 типа

через логарифмы и арктангенсы- в случае простейших дробей 3 типа

через рациональные функции и арктангенсы- в случае простейших дробей 4 типа. Универсальная тригонометрическая подстановка всегда рационализирует подынтегральную функцию, однако часто она приводит к очень громоздким рациональным дробям, у которых, в частности, практически невозможно найти корни знаменателя. Поэтому при возможности применяются частные подстановки, которые тоже рационализируют подынтегральную функцию и приводят к менее сложным дробям.

Формула Ньютона – Лейбница представляет собой общий подход к нахождению определенных интегралов.

Что касается приемов вычисления определенных интегралов, то они практически ничем не отличаются от всех тех приемов и методов.

Точно так же применяются методы подстановки (замены переменной), метод интегрирования по частям, те же приемы нахождения первообразных для тригонометрических, иррациональных и трансцендентных функций. Особенностью является только то, что при применении этих приемов надо распространять преобразование не только на подинтегральную функцию, но и на пределы интегрирования. Заменяя переменную интегрирования, не забыть изменить соответственно пределы интегрирования.

Как следует из теоремы, условие непрерывности функции яв­ляется достаточным условием интегрируемости функции. Но это не означает, что определенный интеграл существует только для непрерывных функций. Класс интегрируемых функций гораздо шире. Так, например, существует определенный интеграл от функ­ций, имеющих конечное число точек разрыва.

Вычис­ление определенного интеграла от непрерывной функции с по­мощью формулы Ньютона-Лейбница сводится к нахождению первообразной, которая всегда существует, но не всегда явля­ется элементарной функцией или функцией, для которой состав­лены таблицы, дающие возможность получить значение интеграла. В многочисленных приложениях интегрируемая функция зада­ется таблично и формула Ньютона - Лейбница непосредственно неприменима.

Если необходимо получить наиболее точный результат, идеально подходит метод Симпсона .

Из выше изученного можно сделать следующий вывод, что интеграл используется в таких науках как физика, геометрия, математика и других науках. При помощи интеграла вычисляют работу силы, находят координаты центр масс, путь пройденный материальной точкой. В геометрии используется для вычисления объема тела, нахождение длины дуги кривой и др.

x i -1/2 =(x i +x i -1)/2 – середина i -го отрезка

Представим на отрезке [x i -1 , x i ] подынтегральную функцию f (x ) в виде полинома третьей степени P i (x ). Этот полином должен быть равен значениям подынтегральной функции в точках сетки и в середине отрезка: P i (x i - 1)=f (x i -1)– равенство полинома значению функции на левой границе i -го отрезка,

P i (x i- 1/2) = f (x i -1/2), P i (x i ) = f (x i ).

Такой полином можно записать, например, следующим образом:

P i (x )=a +b(x-x i -1)+c(x-x i -1)(x-x i -1/2),

здесь a , b, c – неизвестные коэффициенты, подлежащие определению.

Введем обозначение для ширины i -го отрезка: h i =x i -x i -1 ,

тогда (x-x i -1/2)= h i /2, а (x i -1/2 -x i -1)= h i /2.

Запишем значения полинома на левой, правой границах и в середине i -го отрезка

P i (x i ) = a +b*h i + c*h i *h i /2 = f (x i )= f i (1)

P i (x i- 1) = a = f (x i -1)= f i -1 (2)

P i (x i- 1/2)= f (x i -1/2)= a +b*h i /2 = f i -1/2 (3)

Из соотношения (2) следует a = f i -1 ,

из выражения (3) легко увидеть, что b= h i (f i -1/2 - f i )/2,

из выражения (1) получаем c=2 (f i -a -b h i )/h i 2 , подставим в выражение для коэффициента c выражения для коэффициентов a и b, в результате получим:

c=2(f i - f i -1) /h i 2 – (2/h i )(2/h i )(f i -1/2 - f i -1 ) ,

c=2 [f i - f i -1 -2 f i -1/2 +2 f i -1 ] /h i 2 ,

c=2 [f i - 2 f i -1/2 +f i -1 ] /h i 2 .

Подставим найденные коэффициенты a , b, c в выражение для полинома:

P i (x )= f i -1 + 2(f i -1/2 - f i -1)( x -x i -1) /h i + 2 [f i - 2 f i -1/2 +f i -1 ] ( x -x i -1) ( x -x i -1/2)/h i 2

Перейдем от переменной x к переменной t= x -x i -1

Тогда dt = dx , а при x = x i -1 ; t=0, при x = x i ; t=h i при

x = x i -1/2 =x -( x i -x i -1)/2= x -x i /2 -x i -1 /2= x - x i -1 +x i -1 /2-x i /2=t-h i /2

Тогда на i -ом интервале значение интеграла с учетом введенных обозначений, можно записать:

Подставим в выражение для значения коэффициентов a,b и c

Таким образом,

S i – представляет собой значение интеграла на i -ом отрезке. Для получения интеграла на отрезке от a до b, необходимо сложить все S i

Если h i =h для любого i =1,…, N, тогда и формулу Симпсона можно упростить

(4)

Формулу (4) можно упростить, для этого раскроем скобки в выражении под знаком суммирования

Выделим из первой суммы значение функции в точке x =a

,

а из последней суммы – значение функции в точке x =b

В результате получаем рабочую формулу Симпсона для равномерной сетки.

Учтем, что , , получим окончательное выражение для формулы Симпсона

В первой сумме формулы (5) вычисляют сумму значений функции во всех внутренних узлах отрезка , вторая сумма вычисляет сумму значений функции в средних точках i -ых отрезков.

Если середины отрезков включить в сетку наряду с узлами, тогда новый шаг h 0 = h/2 = (b-a)/(2*n), а формула (5) может быть записана в виде:

Рассмотрим . Значение данного интеграла легко найти аналитически и оно равно -0,75. Метод Симпсона для подынтегральной функции в виде полинома степени 3 и ниже дает точное значение.

Алгоритм вычисления этого интеграла методом Симпсона (формула (5)).

цикл по i от 1 до n-1

конец цикла

цикл по I от 1 до n

конец цикла

s=h*(f0+2*s1+4*s2+fn)/6

функция f1

параметры x

возврат x^3+3*x^2 + x*4 - 4

Пример программы вычисления интеграла методом Симпсона на языке VFP (по формуле (6)):

SET DECIMALS TO 10

? "I=",simpson(0,2,20)

PROCEDURE simpson

PARAMETERS a,b,n

S_четные=0

S_нечетные=0

for x=a+h TO b-h STEP 2*h

S_нечетны = S_нечетные + 4*f(x)

for x=a+2*h TO b-h STEP 2*h

S_четные = S_четные + 2*f(x)

S=f(a)*h/3+(S_четные+S_нечетные)*h/3+f(b)*h/3

Пример решения на языке VBA :

"процедура проверки правильности вычисления значения интеграла по его первообразной

s_четные = 0

s_нечетные = 0

For x = a + h To b - h Step 2 * h

s_нечетные = s_нечетные + 4 * f(x)

Debug.Print "s_нечетные = " & s_нечетные

For x = a + 2 * h To b - h Step 2 * h

s_четные = s_четные + 2 * f(x)

Debug.Print "s_четные=" & s_четные

s = h / 3 * (f(a) + (s_четные + s_нечетные) + f(b))

Debug.Print "Метод Симпсона: s= " & s

Debug.Print "Значение первообразной: s_test= ” & s_test(b-a)

Результат работы программы на VBA:

s_нечетные = 79,9111111111111

s_четные=36,0888888888889

Метод Симпсона: s= 2,66666666666667

Значение первообразной: s_test= 2,66666666666667

Контрольные вопросы

1. Что такое определенный интеграл?

2. Привести алгоритм метода прямоугольников.

3. На интервале функция f(x) монотонно возрастает. I 1 – значение интеграла функции f(x) на отрезке , вычисленное по методу левых прямоугольников, I 0 – значение интеграла функции f(x) на отрезке , вычисленное по методу средних прямоугольников. Будут ли отличаться значения интеграла, вычисленные этими методами? Если значения различны, то какое из них больше? Чем определяется разница?

4. Оценить погрешность для вычисления интеграла методом правых прямоугольников для монотонно убывающей функции.

5. Привести алгоритм метода трапеций.

6. Привести алгоритм метода Симпсона.

7. Как определить погрешность вычисления интеграла итерационными методами?

8. Какой из методов имеет наименьшую погрешность вычисления определенного интеграла?

9. Получить формулу метода Симпсона.

Задания

Вычислить следующие интегралы методами: прямоугольников, трапеций, Симпсона с точностью 0,001 и оценить погрешность результатов вычислений этими методами.

2.

3.

4.

5.

10.

11.

14.

18.

Метод трапеций

Разобьем отрезок на равных частей при помощи точек:

Метод трапеций заключается в замене интеграла суммой:

Абсолютная погрешность приближения, полученного по формуле трапеций, оценивается с помощью формулы, где.

Метод парабол (метод Симпсона)

а) Через любые три точки с координатами проходит только одна парабола.

б) Выразим площадь под параболой на отрезке через:

Учитывая значения и из пункта а) следует:

в) Разобьем отрезок на равных частей при помощи точек:

Метод парабол заключается в замене интеграла суммой:

Для приближенных практических расчетов применяется формула:

Абсолютная погрешность вычисления по формуле (4) оценивается соотношением, где.

Оценка точности вычисления «неберущихся» интегралов

В данной работе вычисление абсолютной и относительной погрешности проводится при условии, что известно точное значение определенного интеграла. Однако не всякая первообразная, даже тогда, когда она существует, выражается в конечном виде через элементарные функции. Таковы первообразные, выраженные интегралами, и т.д. Во всех подобных случаях первообразная представляет собой некоторую новую функцию, которая не сводится к комбинации конечного числа элементарных функций.

Определенные интегралы от таких функций можно вычислить только приближенно. Для оценки точности вычисления в таких случаях используют, например, правило Рунге. В данном случае интеграл вычисляется по выбранной формуле (прямоугольников, трапеций, парабол Симпсона) при числе шагов, равном n, а затем при числе шагов, равном. Погрешность вычисления значения интеграла при числе шагов, равном, вычисляется по формуле Рунге:, для формул прямоугольников и трапеций, а для формулы Сипсона. Таким образом, интеграл вычисляется для последовательных значений числа шагов, ..., где - начальное число шагов. Процесс вычислений заканчивается, когда для очередного значения будет выполнено условие, где - заданная точность.

Для того чтобы не вычислять один и тот же интеграл по нескольку раз для разных разбиений отрезка интегрирования, можно вычислить шаг интегрирования заранее.

Пример. Выбрать шаг интегрирования для вычисления интеграла с точностью 0,01 пользуясь квадратурными формулами прямоугольников, трапеций, Симпсона.

Квадратурная формула прямоугольников.

Вычислим, при каком шаге погрешность будет составлять 0,01:

подынтегральный трапеция парабола неберущийся

Поскольку, то.

При шаге отрезок разбивается на равностоящих узлов.

Квадратурная формула трапеций.

Поскольку, .

При шаге,отрезок разбивается на равностоящих узлов.

Квадратурная формула Симпсона.

Вычислим, при каком шаге погрешность составит 0,01:

При шаге, отрезок разбивается на равностоящих узлов.

Как и следовало ожидать, наименьшее количество равностоящих узлов получается при вычислении интеграла по квадратурной формуле Симпсона.

Студенту предлагается работа, состоящая из четырех этапов:

• 1 этап - точное вычисление определенного интеграла.
• 2 этап - приближенное вычисление определенного интеграла одним из методов: прямоугольников или трапеций.
• 3 этап - приближенное вычисление определенного интеграла методом парабол.

4 этап - расчет и сравнение абсолютной и относительной ошибок приближенных методов: , где - точное решение интеграла, - значение интеграла, полученное с помощью приближенных методов.

Построение графика подынтегральной функции.

Варианты и образец выполнения РГР приведены ниже.

Варианты

№ варианта

Образец выполнения РГР

Задание. Вычислить интеграл

1. Точное вычисление:

2. Приближенное вычисление с помощью формул прямоугольников:

Составим таблицу:

По первой формуле прямоугольников получаем:

0,1 = 0,1·3,062514 = 0,306251.

По второй формуле прямоугольников получаем:

0,1 = 0,1· 4,802669 = 0,480267.

В данном случае первая формула дает значение интеграла с недостатком, вторая - с избытком.

3. Приближенное вычисление по формуле трапеций:

В нашем случае получаем:

0,1 = =0,1 = 0,1·4,095562 = =0,409556.

Вычислим относительную и абсолютную погрешности.

4. Приближенное вычисление по формуле Симпсона:

В нашем случае получаем:

Вычислим относительную и абсолютную погрешности.

В действительности, = 0,40631714.

Таким образом, при разбиении отрезка на 10 частей по формуле Симпсона мы получили 5 верных знаков; по формуле трапеций - три верных знака; по формуле прямоугольников мы можем ручаться только за первый знак.

Остаточный член квадратурной формулы Симпсона равен , где ξ∈(x 0 ,x 2) или

Назначение сервиса . Сервис предназначен для вычисления определенного интеграла по формуле Симпсона в онлайн режиме.

Инструкция . Введите подынтегральную функцию f(x) , нажмите Решить. Полученное решение сохраняется в файле Word . Также создается шаблон решения в Excel .

Правила ввода функции

Примеры правильного написания F(x):
1) 10 x e 2x ≡ 10*x*exp(2*x)
2) x e -x +cos(3x) ≡ x*exp(-x)+cos(3*x)
3) x 3 -x 2 +3 ≡ x^3-x^2+3

Вывод формулы Симпсона

Из формулы
при n = 2 получаем

Т.к. x 2 -x 0 = 2h, то имеем . (10)
Это формула Симпсона . Геометрически это означает, что кривую y=f(x) мы заменяем параболой y=L 2 (x), проходящей через три точки: M 0 (x 0 ,y 0), M 1 (x 1 ,y 1), M 2 (x 2 ,y 2).

Остаточный член формулы Симпсона равен

Предположим, что y∈C (4) . Получим явное выражение для R . Фиксируя среднюю точку x 1 и рассматривая R=R(h) как функцию h, будем иметь:
.
Отсюда дифференцируя последовательно три раза по h , получим






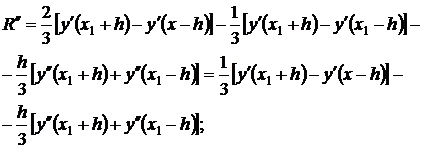
Окончательно имеем
,
где ξ 3 ∈(x 1 -h,x 1 +h). Кроме того, имеем: R(0) = 0, R"(0)=0. R""(0)=0. Теперь, последовательно интегрируя R"""(h), используя теорему о среднем, получим


Таким образом, остаточный член квадратурной формулы Симпсона равен
, где ξ∈(x 0 ,x 2). (11)
Следовательно, формула Симпсона является точной для полиномов не только второй, но и третьей степени.
Получим теперь формулу Симпсона для произвольного интервала [a ,b ]. Пусть n = 2m есть четное число узлов сетки {x i }, x i =a+i·h, i=0,...,n, и y i =f(x i). Применяя формулу Симпсона (10) к каждому удвоенному промежутку , ,..., длины 2h , будем иметь


Отсюда получаем общую формулу Симпсона
.(12)
Ошибка для каждого удвоенного промежутка (k=1,...,m) дается формулой (11).

Т.к. число удвоенных промежутков равно m , то

С учетом непрерывности y IV на [a ,b ], можно найти точку ε, такую, что .
Поэтому будем иметь
. (13)
Если задана предельно допустимая погрешность ε, то, обозначив , получим для определения шага h
.
На практике вычисление R по формуле (13) бывает затруднительным. В этом случае можно поступить следующим образом. Вычисляем интеграл I(h)=I 1 с шагом h , I(2h)=I 2 с шагом 2h и т.д. и вычисляем погрешность Δ:
Δ = |I k -I k-1 | ≤ ε. (14)
Если неравенство (14) выполняется (ε - заданная погрешность), то за оценку интеграла берут I k = I(k·h).
Замечание. Если сетка неравномерная, то формула Симпсона приобретает следующий вид (получить самостоятельно)
.
Пусть число узлов n = 2m (четное). Тогда

где h i =x i -x i-1 .

Пример №1 . С помощью формулы Симпсона вычислить интеграл , приняв n = 10.
Решение: Имеем 2m = 10. Отсюда . Результаты вычислений даны в таблице:

i	x i	y 2i-1	y 2i
0	0		y 0 = 1.00000
1	0.1	0.90909
2	0.2		0.83333
3	0.3	0.76923
4	0.4		0.71429
5	0.5	0.66667
6	0.6		0.62500
7	0.7	0.58824
8	0.8		0.55556
9	0.9	0.52632
10	1.0		y n =0.50000
∑		σ 1	σ 2

По формуле (12) получим .
Рассчитаем погрешность R=R 2 . Т.к. , то .
Отсюда max|y IV |=24 при 0≤x≤1 и, следовательно . Таким образом, I = 0.69315 ± 0.00001.

Пример №2 . В задачах вычислить определенный интеграл приближенно по формуле Симпсона, разбив отрезок интегрирования на 10 равных частей. Вычисления производить с округлением до четвертого десятичного знака.

Метод секущих можно рассматривать как замену функции интерполяционным многочленом первой степени, проведенным по узлам

По трем последним итерациям можно построить интерполяционный многочлен второй степени, т. е. заменить график функции параболой. Запишем интерполяционный многочлен в форме Ньютона

Приравнивая его нулю, получим квадратное уравнение

Тот из двух корней квадратного уравнения (36), который меньше по модулю, определяет новое приближение

Очевидно, для начала расчета надо задать три первых приближения (обычно наугад выбирают три числа), т. е. процесс является трехшаговым.

Метод парабол построен по образцу методов третьего порядка. Однако замена производных разделенными разностями приводит к существенному уменьшению скорости сходимости. Рассуждениями, аналогичными рассуждениям в п. 7, можно показать, что вблизи простого корня выполняется соотношение

т. е. сходимость даже медленнее квадратичной. Вблизи кратного корня сходимость еще медленнее (хотя и более быстрая, чем линейная). Заметим, что строить аналогичные методы с использованием интерполяционного многочлена еще более высокой степени невыгодно: сходимость все равно будет медленней квадратичной, а расчет сильно усложняется.

В методе парабол «разболтка» счета вблизи корня сказывается еще сильней, чем в методе секущих, ибо в расчете участвуют вторые разности. Тем не менее корни можно найти, с хорошей точностью; для определения оптимального числа итераций удобно пользоваться приемом Гарвика, описанном в п. 7.

Метод парабол имеет важное достоинство. Даже если все предыдущие приближения действительны, уравнение (36) может привести к комплексным числам. Поэтому процесс может естественно сойтись к комплексному корню исходного уравнения. В методах простых итераций, касательных или секущих для сходимости к комплексному корню может потребоваться задание комплексного начального приближения (если ) вещественна при вещественном аргументе).

Корни многочлена. Метод парабол оказался исключительно эффективным для нахождения всех корней многочлена высокой степени. Если - алгебраический многочлен, то, хотя сходимость метода при произвольном начальном приближении и не доказана, на практике итерации всегда сходятся к какому-нибудь корню, причем быстро.

Для многочлена частное есть тоже многочлен; поэтому последовательно удаляя найденные корни, можно найти все корни исходного многочлена.

Замечание 1. Если - многочлен высокой степени, то возникают дополнительные трудности. Многочлен быстро возрастает при увеличении аргумента, поэтому в программе для ЭВМ должна быть страховка от переполнения. Обычно вводят масштабные множители, величина которых связана с диапазоном изменения аргумента.

Замечание 2. Наибольшие по модулю корни многочлена высокой степени могут быть очень чувствительны к погрешности коэффициентов при старших степенях. Например, корнями многочлена

являются последовательные целые числа слегка измененный многочлен имеет такие корни:

(здесь приведен только один знак после запятой). Кратные или близкие корни могут быть слабо устойчивыми даже при меньших степенях многочлена.

Замечание 3. Для удаления вычисленных корней надо... делить многочлен. Это вносит погрешность округления в коэффициенты и влияет на точность нахождения следующих корней. На практике отмечено, что если сначала удалять меньшие по модулю корни, точность падает мало, но если надать удаление с больших корней, точность может упасть катастрофически. Поэтому за начальное приближение берут тогда итерации обычно сходятся к наименьшему по модулю корню. Его удаляют и по такому же начальному приближению ищут следующий корень и т. д. При такой организации вычислений потеря точности будет небольшой.